Dissipation Time for Wound Roll

Published: August 26, 2014, By Kelly Robinson

I received an interesting question. A wound roll of biaxially oriented polypropylene (BOPP) has high static. To get rid of the static, we plan to put the roll on a concrete floor and let it sit for a week. Won’t this get rid of the static?

The quick answer is no. Charge persists on wound rolls of polypropylene for weeks, months, or longer. The best solution is to improve static control so that no static is wound into the roll.

The longer answer is to analyze an idealized geometry. Static electricity has a long history of investigation. Workers contribute to our understanding by writing about their observations and thoughts. We benefit from their work by applying their observations and thoughts to our applications. Let's analyze an idealized geometry and see how long it takes for static to dissipate. However, what idealized problem makes sense?

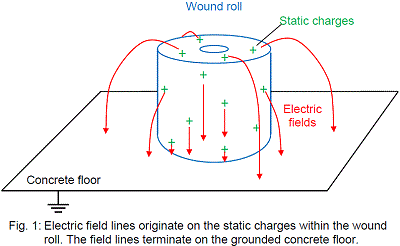
The factory floor geometry in Figure 1 shows the wound roll sitting on the concrete floor. Static charges are distributed throughout the wound roll. Electric field lines that originate on the static charges within the wound terminate on the grounded concrete floor. Most concrete floors built since about 1950 are well grounded. I have seen only one concrete aggregate floor that was insulating. And, this floor dated back to ~1870 when the original factory building was built.

 The factory floor geometry in Figure 1 is so complex that I’d use a computer running one of the powerful finite element method programs to find how long charge dissipation would take. A good alternative is to analyze a model geometry that has two important features.

 First, it must include the mechanism for charge dissipation; electrical conduction.

 Second, it must be simple enough so that I can estimate the time needed for charge to dissipate.

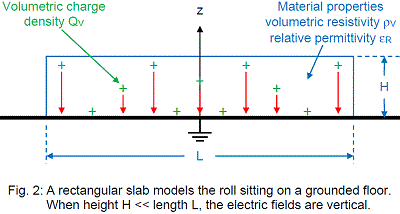
 One idealized geometry in Figure 2 that has these two features is a rectangular slab on a grounded plane. The slab models the charge roll. One compromise is that our idealized geometry is flatter than the actual geometry. The height H of the slab is smaller than the length L and rolls usually have a width that is about the same as the roll diameter. So, our estimate of the charge dissipation time for the model geometry may be somewhat different from the time needed for our roll. None-the-less, we should get a pretty good “ball park” estimate.

The electric fields within the slab are found using the Poisson equation in (3) where the permittivity ε is a material property and Q_V is the volumetric charge density within the roll.

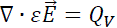      (3)

In our idealized geometry, the electric fields are vertical. That is, they have only a z component. So, (3) simplifies to 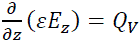(4)

      (4)

Next, we’ll assume that our wound roll is homogeneous. This approximation is OK when the web has no coatings. In this case, the permittivity e is uniform (does not vary with z) and (4) simplifies to 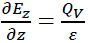(5).

     (5)

Next, we’ll keep things simple and assume that the charge density Q_V is uniform. This simplifying assumption is OK if charge on the web was uniform when the roll was wound. If not, this assumption considers only the average charge. With this assumption, (5) simplifies to 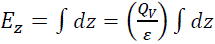(6).

     (6)

Now, we can integrate to find the electric field as a function z in 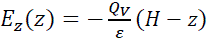(7).

     (7)

Since there is no charge above the roll, the electric field at height H in (7) must be zero.

Our solution for the electric field is sensible. The field is proportional to the charge density Q_V. More charge means higher fields. And, the field is maximum at the bottom of the roll that touches the floor.

Now that we know the electric field within our idealized geometry, we can find the time needed for charge to dissipate. Moving charge is current. And, the current density J is proportional to the electric field E. This approximation in (8) is Ohm’s law.

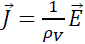     (8)

The constant of proportionality ρ_V is the electrical resistivity of our material. The actual charge movement in most insulators varies strongly with electric field. So, this assumption leads to a severe under estimate of the charge dissipation time. None-the-less, let’s use it and follow through with the analysis.

Conservation of charge in (9) requires that the volumetric charge density Q_V of any little volume within the slab must go down when charge moves out of the volume.

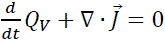     (9)

In our idealized geometry, the electric fields have only a z component, and (9) simplifies to 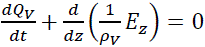(10).

     (10)

Using (7), (10) simplifies to 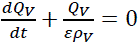(11).

     (11)

The solution for (11) is well known. The charge density Q_V in (12) decreases exponentially with time.

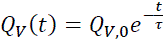     (12)

The charge relaxation time τ in (12) is given in 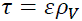(13).

     (13)

Note that the charge relaxation time τ is independent of the height H and width W of the slab. The key result of our analysis is that the charge relaxation time is a material property.

 For polypropylene, the dielectric constant is about 2.2. While the volumetric resistivity varies, it is on the order of 10⁺¹⁷ W-cm. The charge relaxation time for polypropylene in (14) is about 5.4 hours.

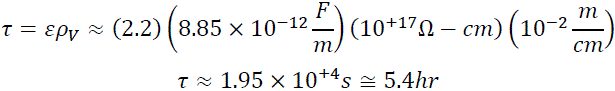
Our analysis estimates that 95% of the initial charge should dissipate from our wound roll of polypropylene in about 3 time constants or about a day. My experience is that this analysis severely underestimates the charge dissipation time by a factor of at least 100X. Charge persists on wound rolls of polypropylene for weeks or months. Ohmic conduction is a very poor approximation for charge movement in polypropylene. african porn videos

I invite you to ask questions about this blog and to suggest future topics. My email address is: This email address is being protected from spambots. You need JavaScript enabled to view it..