Static Beat | Static Dissipator Neutralization Efficiency
- Published: January 03, 2014, By Kelly Robinson
When do you need static bars with high static dissipation performance?
Static charges can cause a number of problems including sparks that ignite fires, shock people, and cause logic errors. Static charges cause sheets to stick and attract airborne contaminates. Many static dissipators are commercially available for controlling static on webs and sheets. Static dissipators are either “passive” or “active.” Passive dissipators, like static brushes, tinsel, or ionizing cords, are less expensive, while active dissipators, such as static bars or radioactive alpha emitters, have higher static dissipation performance.
When can you save money by using passive dissipators? And when should you pay for the higher performance of active static bars? To make an informed decision, let’s analyze the performance of a static dissipator used to neutralize the charges on the web in Figure 1 and discover that three key parameters determine the neutralization efficiency—our static bar, how well we install our static bar, and our process:
- The number of corona ions nION produced by the static dissipator (our static bar)
- The length of the web LION within the ionization field of the ionizer (our installation)
- The web speed UWEB (our process)
For our analysis, let’s look at the neutralization efficiency of the static bar Figure 1. The web enters with static charge density σWEB and moves past the static bar at speed UWEB. The static bar on the grounded metal machine frame generates both positive and negative corona ions in spherical regions near the tips of each pin. The electric field E from the positive static charges on the web within the ion field length LION reach the static bar and attract negative corona ions from the active static bar across gap G. The positive corona ions are repelled by the electric field and move toward the grounded plate.
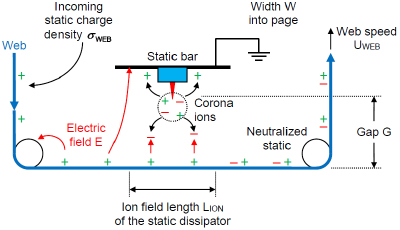
My blog post presents the analysis showing that the static charge on the web σWEB in Equation 2 dissipates exponentially with time.
![]()
Equation 2: The static charge σWEB dissipates exponentially with time constant τDISSIPATOR.
The ratio of the web exposure time TWEB to the dissipator time constant τDISSIPATOR determines the time constant. The electric Reynolds number Re, the ratio of the time constant τDISSIPATOR to the mechanical exposure time TWEB, is an important dimensionless number that appears often in applied electrostatics.
The neutralization efficiency ηDISSIPATOR in Equation 3 depends on the electric Reynolds number Re.
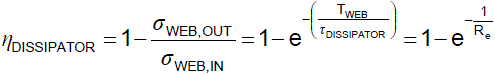
Equation 3. The neutralization efficiency ηDISSIPATOR depends on the electric Reynolds number Re.
The neutralization efficiency is determined by the electric Reynolds number Re in Equation 4. Smaller Re is better.
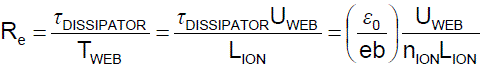
Equation 4: The web speed UWEB, the web length exposed to ions LION, and the ion density nION generated by the dissipator determine the neutralization efficiency ηDISSIPATOR.
Equation 4 is the key result showing us how we can maximize the performance of our static dissipators by making this ratio as small as possible. The terms in parentheses are physical constants. The three following terms are design factors that determine performance:
- First, choose a high performance static dissipator. Static dissipators generate ions. More ions (bigger ion density nION) are better. Better static bars have more pins, have sharper pins that stay clean, and use power supplies with higher voltages. Most static bars operate at 4KV. Higher performance static bars operate at 7KV. As static bars age, their ion output goes down. nION decreases and the neutralization efficiency ηDISSIPATOR suffers. Cleaning the pins increases performance by removing debris that makes the pin dull. Some high performance static bars keep the pin tips clean using air flow across the pins.
- Next, install the static dissipator in an effective location. Install your static dissipator to maximize the distance LION that the web in Figure 5 is exposed to ions from the static dissipator. The edges of the region exposed to ions are found by drawing a cylinder centered on the web that just touches the static dissipator and the closest grounded objects, which are the metal idler rollers. So, install your static dissipator midway between idlers away from machine frames. Notice that installing your static dissipator close to the web (making the gap G small) is not important. Rather, set the gap G to maximize LION.
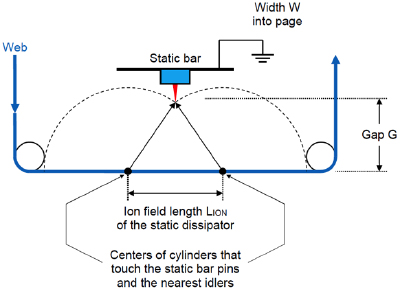
Figure 5. The installation geometry determines the distance LION that the web is exposed to ions from the static dissipator.
- Finally, from Equation 4, static dissipator performance decreases as the web speed increases. High performance static dissipaters can be effective at web speeds up to about 500 m/min. Of course, the static dissipaters must be installed in effective locations. To control static when your web speed exceed 500 m/min, you may need to use pairs of static dissipator.
The static neutralization efficiency of static dissipators is determined by 3 factors:
- The number of ions generated by the static dissipator,
- Installing our static dissipator to maximize the web distance exposed to ions, and
- The web speed.
Higher performance static dissipaters form more ions. They have more static pins, the pins are sharper, and they operate at higher voltage. Our static dissipator must be installed in an effective location so that the web distance exposed to ions is maximized. Finally, static dissipator performance decreases as the web speed increases.
I invite you to ask questions about this column and to suggest future topics. My email address is: Kelly.Robinson@ElectrostaticAnswers.com.
Static control expert Dr. Kelly Robinson, president of Electrostatic Answers, has 27+ years of experience in problem-solving and consulting. Kelly writes PFFC's Static Beat column and the Kelly on Static blog. Contact him at 585-425-8158; kelly.robinson@electrostaticanswers.com; www.electrostaticanswers.com.














