Static Dissipator Performance
- Published: December 24, 2013, By Kelly Robinson
1. SUMMARY
We will find that (1) the better static bars produce more ions, and (2) that better installation exposes a longer web distance to the corona ions from our dissipator. The key quantitative result is Equation 8.
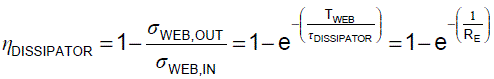
Equation 8: For better static dissipator efficiency ηDISSIPATOR,
the time TWEB that the web is exposed to the dissipator
should be bigger and the dissipator time constant
τDISSIPATOR should be smaller.
The neutralization efficiency ηDISSIPATOR is determined by the electric Reynolds number Re in Equation 9 that includes the web speed UWEB, the number density of ions nION produced by our static dissipator, and the web distance LION that is exposed to corona ions from our dissipator.
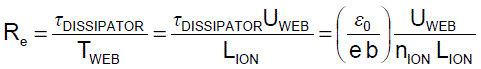
Equation 9: The electric Reynolds number Re
determines dissipator performance.
The quantities in parentheses are constants. Following are the design parameters that we control that determine the dissipator neutralization efficiency.
2. GEOMETRY
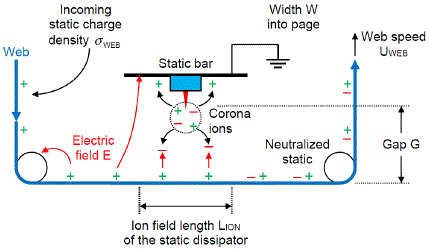
Figure 1. The static dissipator generates positive and negative
corona ions. The negative ions move across the gap G
to neutralize the positive static charges on the web.
Let’s analyze the performance of a static dissipator used to neutralize the charges on the web in Figure 1. The web enters with static charge density σWEB and moves past the static bar at speed UWEB. The static bar on the grounded metal machine frame generates both positive and negative corona ions near the tips of each pin. The electric field E from the positive static charges on the web within the ion field length LION reach the static bar and attract negative corona ions from the active static bar across gap G. The positive corona ions are repelled by the electric field and move towards the grounded plate.
3. ANALYSIS
To estimate the neutralization efficiency, let’s look at the flow of corona ions from the static dissipator to the charged web. The current density JION in Equation 2 is proportional to the electric field E.
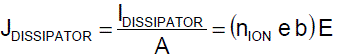
Equation 2: The current density JDISSIPATOR is proportional
to the electric field E.
The static dissipator generates ions with a number density nION each having charge e and electric mobility b. The number of ions nION is the key performance metric for the static dissipator. More ions are better. Most corona ions carry one electronic charge (e=1.6×10-19 C). Corona ions in air have a mobility of about 3×10-4 m2/(V-sec).
We can find the effective resistance of the ion flow by estimating the electric field using Equation 3.
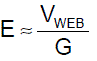
Equation 3: The electric field E is estimated to be
the web voltage VWEB divided by the gap G.
Use Equation 2 and Equation 3 to find the dissipator resistance RDISSIPATOR in
Equation 4.
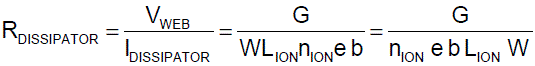
Equation 4: The dissipator resistance RDISSIPATOR
is the ratio of web voltage VWEB
to dissipator current IDISSIPATOR.
Equation 4 is sensible. The dissipator resistance RDISSIPATOR is larger when the gap G is larger. And RDISSIPATOR is smaller when our dissipator produces more ions nION.
To find the time required to neutralize the web, we need to know the web capacitance. The capacitance between the web and the static dissipator is estimated in Equation 5 using a parallel plate approximation.
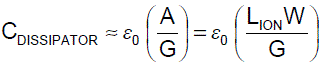
Equation 5: The capacitance CDISSIPATOR between the web
and the static dissipator is estimated
using a parallel plate approximation.
Equation 5 is also sensible. The capacitance is smaller when the gap G is bigger.
Finally, the time constant τ governing the dissipation of the web static is found in Equation 6.
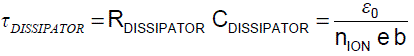
Equation 6: Time constant τDISSIPATOR governs
the dissipation of web static.
Finding the dissipator time constant τDISSIPATOR in Equation 6 is a key result. The time constant τDISSIPATOR governing static dissipation by a static dissipator depends only on the number of ions nION generated by the dissipator.
Wow! The dissipation time constant is determined solely by the design of the static dissipator and does not depend on how the dissipator is installed. Specifically, the gap G and web length LION do not appear on Equation 6.
Web static σWEB in Equation 7 dissipates exponentially with time.
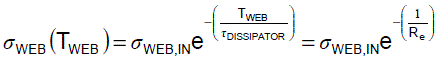
Equation 7: Web static σWEB dissipates exponentially with time.
4. NEUTRALIZATION EFFICIENCY
When the web exits with zero static in Equation 8 (σWEB-OUT=0), the static dissipator efficiency nDISSIPATOR is 100%.
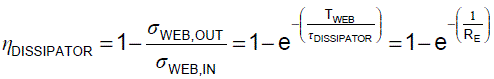
Equation 8: For better static dissipator efficiency nDISSIPATOR,
the time ΤWEB that the web is exposed
to the dissipator should be bigger and
the dissipator time constant τDISSIPATOR
should be smaller.
The electric Reynolds number Re in Equation 9 determines how much charge is dissipated.
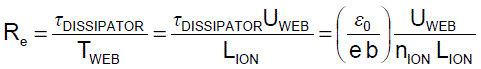
Equation 9. The electric Reynolds number Re determines performance.
The quantities in parentheses are constants. So, the neutralization efficiency is determined by the web speed UWEB, the number density of ions nION, and the web length LION that is exposed to the flow of ions.
Equation 9 is sensible. For higher efficiency nDISSIPATOR, the electric Reynold's number Re should be smaller. So, static neutralization efficiency is better when the web speed UWEB is slower, when the number of ions nION from our dissipator is higher, and when the web length LION exposed to ions is larger.
5. DISSIPATOR INSTALLATION
Clearly, installing the static dissipator is important. A better static dissipator installation makes LION larger. Distance LION in Figure 10 depends on the installation geometry. To determine LION, in your mind's eye, draw a pencil line across the web. This line is the center of a cylinder that expands radially. The two lines in Figure 10 are the centers of cylinders that touch the tips of the dissipator pins and also just touch the idler rollers.
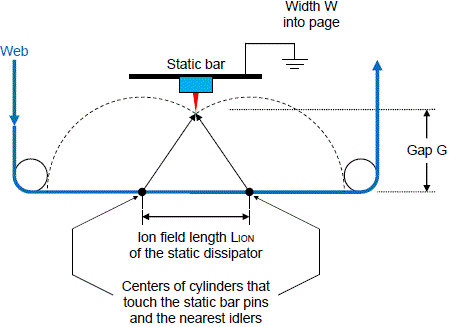
Figure 10. Install static dissipators to maximize the distance LION
that the web is exposed to corona ions.
6. CONCLUSIONS
Our analysis provides two key insights.
- Better static bars produce more ions. Look for static bars that have more pins, that have sharper pins, and that have higher operating voltages.
- Better installations expose longer web spans to corona ions. A better installation has a longer LION, which is the web span exposed to corona ions from the static dissipator. Playing online casino slots is one of the greatest methods to start gambling. Most online casinos provide a variety of slot games presented here to play without having to make a payment. Free games allow you to concentrate on the game while learning casino lobby without risking your hard-earned cash. After you've gained some confidence, you may try your hand at real-money slot machines.
And, our analysis provides one key quantitative result. The neutralization efficiency nDISSIPATOR in Equation 8 depends on the electric Reynolds number Re in Equation 9. In summary, the neutralization efficiency is determined by the web speed UWEB, the number of ions NION generated by the static dissipator, and the distance LION that the web is exposed to corona ions.
I invite you to ask questions about this column and to suggest future topics. My e-mail address is This email address is being protected from spambots. You need JavaScript enabled to view it..




